In the rapidly evolving field of blockchain technology, scalability remains a critical challenge. Zero-knowledge proofs (ZKPs) have emerged as a promising solution to enhance scalability. This article delves into the fundamental concepts of zero-knowledge proofs and their pivotal role in addressing scalability issues on blockchains. Specifically, it focuses on zkEVMs (zero-knowledge Ethereum Virtual Machines), which integrate ZKPs to facilitate a more scalable and secure blockchain. By providing a comprehensive comparison between various notable zkEVM implementations, the article aims to elucidate their differences and advantages.
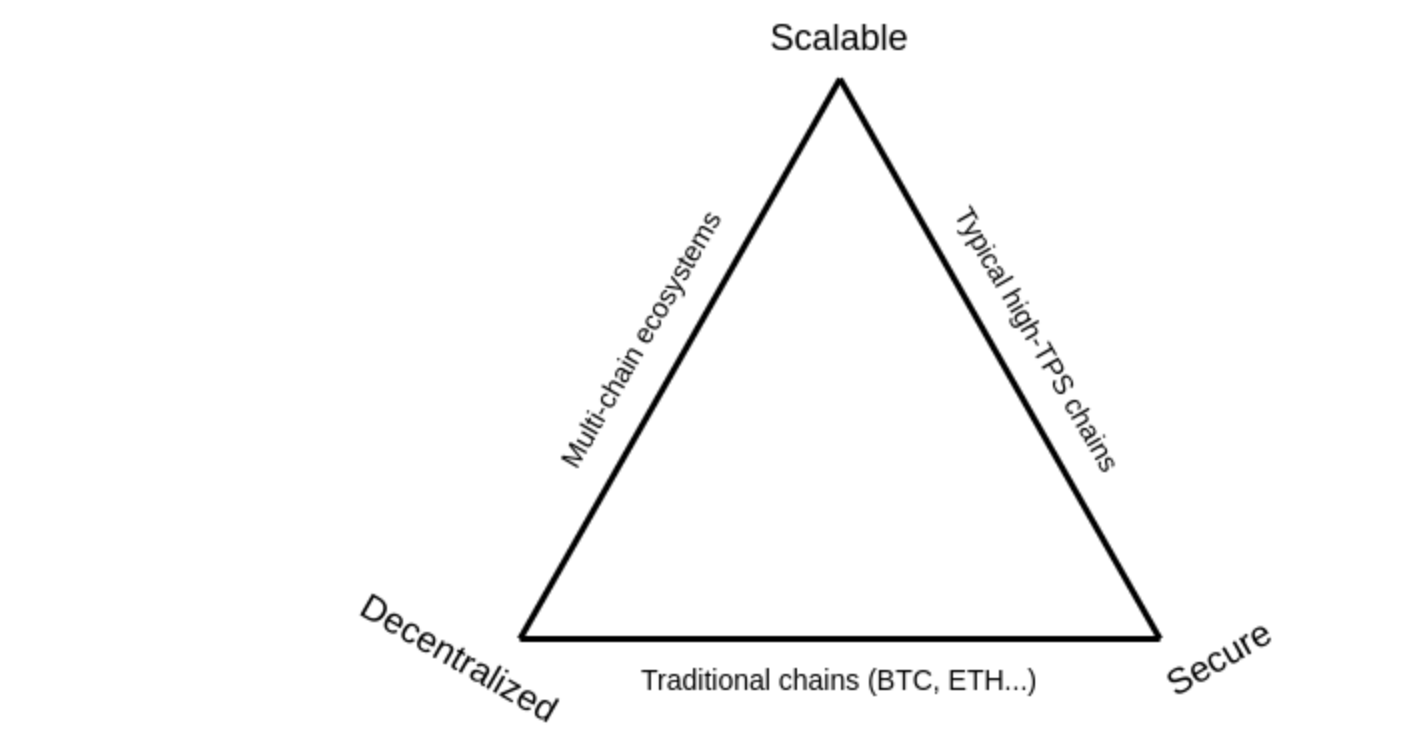
Blockchain trilemma
Blockchain trilemma (first coined by Vitalik Buterin) is a problem faced by blockchain engineers. The trilemma states that we cannot optimize all three aspects of a blockchain, namely, decentralization, security and scalability without accepting some kind of trade-off between them. Traditional blockchains like Bitcoin, Ethereum, etc are built upon security and decentralization. Therefore, they inevitably suffer from scalability problems. Recognizing this problem, the Ethereum team has proposed a rollup-centric roadmap to scale the blockchain through rollups.
Similar to how the Internet protocol is modelled as a multi-layer stack, a blockchain protocol can be divided into several layers.
- Layer 0 (L0): consists of hardware devices, protocols, connections, and other components that form the foundation of a blockchain ecosystem, Layer 0 acts as the infrastructure lying underneath the blockchain.
- Layer 1 (L1): carries out most of the tasks to maintain a blockchain network’s fundamental operations like consensus mechanisms, dispute resolution, programming languages, policies, etc. This layer represents the actual blockchain.
- Layer 2 (L2): is an extra layer sitting on top of layer-1. Layer 2 performs the majority of transactional validations and heavy computations that are meant to run on layer 1. Layer 2 relies on layer 1 for security, so it frequently exchanges data with layer 1.
Scaling using rollups - layer 2
Scaling solutions refer to protocols that help solve the scalability problem of blockchain. A solution can be implemented on any layer of the blockchain, however, L0 and L1 are costly to modify as some changes might require a hard fork. Nowadays, the most widely adopted scaling solutions are implemented on L2 and many of them are rollups.
Rollup is a class of L2 scaling solutions that bundles several off-chain transactions into one on-chain commitment, hence reducing the overall cost of the protocol as fewer computations are performed on L1. According to how rollups enforce Computational Integrity (CI), there are two main types of rollups:
- In optimistic rollups, L2 sequencers submit batches of transactions to the mainnet without verifying their validity. Instead of immediate verification, optimistic rollups provide a challenge period, lasting up to approximately seven days, during which network participants can dispute the validity of any transaction.
- Zero-knowledge (ZK) rollups use advanced cryptographic techniques known as zero-knowledge proofs to validate transactions. This method allows the execution of transactions on L2 to be verified on L1 without a challenge period, significantly improving the user experience for cross-chain transactions between L1 and L2 compared to optimistic rollups.

In this article, we focus on ZK rollups (zkEVM). First, we explore the concept of zero-knowledge proof (ZKP). Then, we delve into how ZKP can improve the scalability of blockchain. Finally, we summarize and compare some existing implementations zkEVM, evaluating their designs and performance.
What is zero-knowledge proof?
Zero-knowledge proof is first devised in 1985 by Goldwasser, Micali, and Rackoff, as an interactive proof system (IP) is an interactive protocol that involves two parties: a prover and a verifier. These two parties will communicate back and forth multiple times for prover to convince verifier that a statement is true. Any interactive proof has the two following properties:
- Completeness: If the statement is true, then an honest prover can convince the verifier with high probability.
- Soundness: If the statement is false, then, for any prover, the verifier rejects the proof with high probability.
If prover only sends one message to verifier, we say that the proof system they engaged in is non-interactive. One of the most employed cryptographic techniques to turn interactive proof systems into non-interactive protocols is Fiat-Shamir transformation.
In practice, the term "proof" is used interchangeably with "argument" and, most of the times, the latter is more accurate. Argument systems were introduced by Brassard, Chaum, and Crépeau in 1986. Compared to proof systems, the soundness property of argument systems is only required to hold against computationally bounded provers (provers with limited computing resources). According to this intuition, most modern computers are bounded, so arguments are considered "sound enough" in most cases.
A proof or argument system is considered zero-knowledge if the prover discloses nothing to the verifier other than the truthfulness of the statement being proved. A witness for a statement is a piece of information that allows you to efficiently verify that the statement is true. In a zero-knowledge proof system, prover can convince verifier that the existential statement holds while revealing absolutely no information about any of the witnesses.
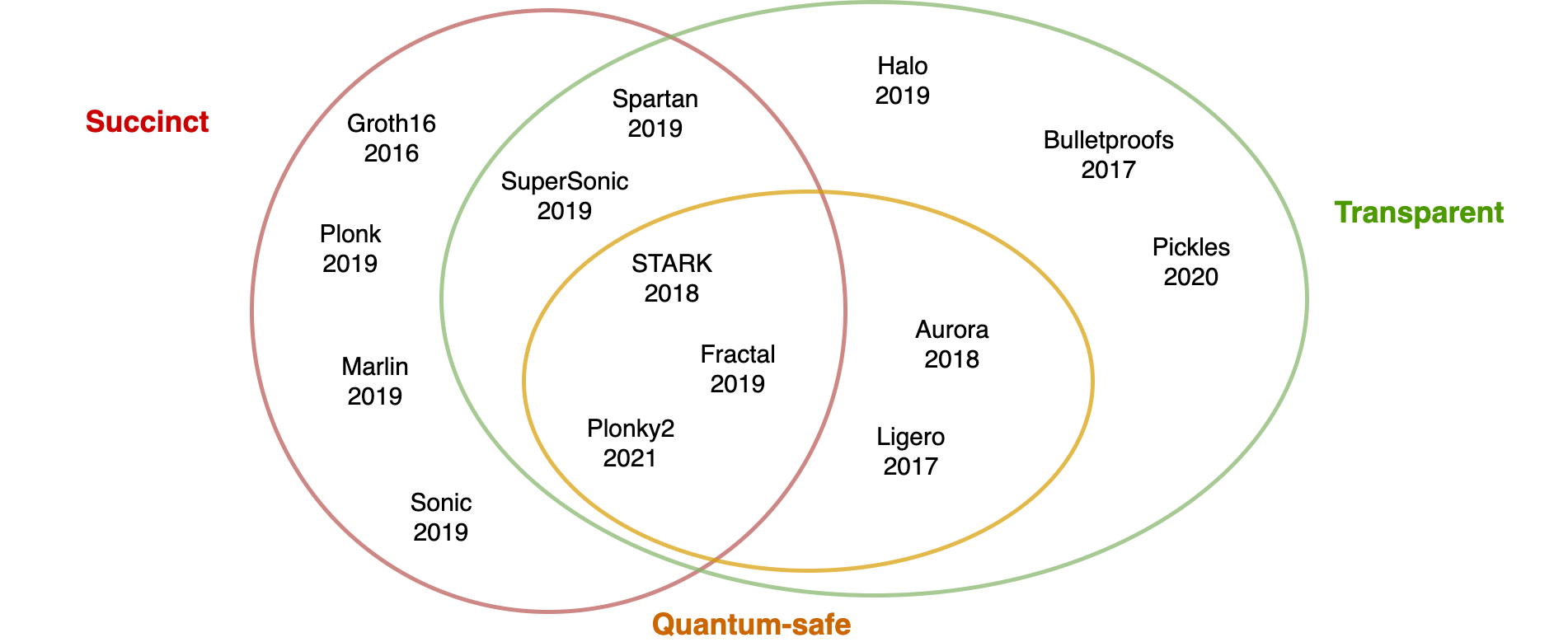
Currently, many practical zero-knowledge proof (or argument) systems have been realized. Most of these schemes fall into one of the two following categories:
- Zero-Knowledge Succinct Non-Interactive Argument of Knowledge (zk-SNARK):
- Zero-Knowledge Scalable Transparent Arguments of Knowledge (zk-STARK):
The main difference between zk-SNARK and zk-STARK is the need for trusted setup - a piece of random data that must be honestly generated. In reality, randomness generation is not easy to implement securely, especially in a trustless setting (you can look at Zcash's counterfeiting vulnerability). zk-STARK eliminates the need for trusted setup, which effectively reduces security risks and assumptions while increasing protocol's transparency. On the other hand, zk-STARKs usually have significantly larger proof size compared to that of zk-SNARKs. This can be a big problem if data transfer is expensive like in the case of Ethereum smart contracts. Therefore, both zk-SNARKs and zk-STARKs are sometimes utilized in one protocol to get the best of both worlds, e.g., Plonky2 [7], eSTARK [8], etc.
Zero-knowledge proof is a fast-growing field of research and the race to practical and efficient general-purpose ZKPs is reaching new heights (a Cambrian explosion as described by Eli Ben-Sasson) with the rise of zero-knowledge Virtual Machines (zkVMs).
How do ZKPs improve scalability on blockchain?
How are zero-knowledge proofs of any help towards blockchain scalability? One of the most desired properties of zero-knowledge proofs is succintness - the ability to prove a statement with a proof much smaller than witness. For example, a prover can convince verifier that he has correctly run a computation against a massive database (a few GB) without revealing the whole database to verifier. It is as if prover has "compressed" the database into a small piece of proof (a few hundred bytes). Moreover, advanced techniques like recursion, aggregation or composition can be applied to further minimize the proof size. It is also important that zero-knowledge proof verification is most likely to be cheaper and faster than naively re-running the computation (naive verification).
Since L1 blockchains are highly secure, we can trust a smart contract (that is carefully audited) to run proof verification for us. This is the most common approach when designing a ZK rollup. Generally, a simplified ZK rollup looks something like this:
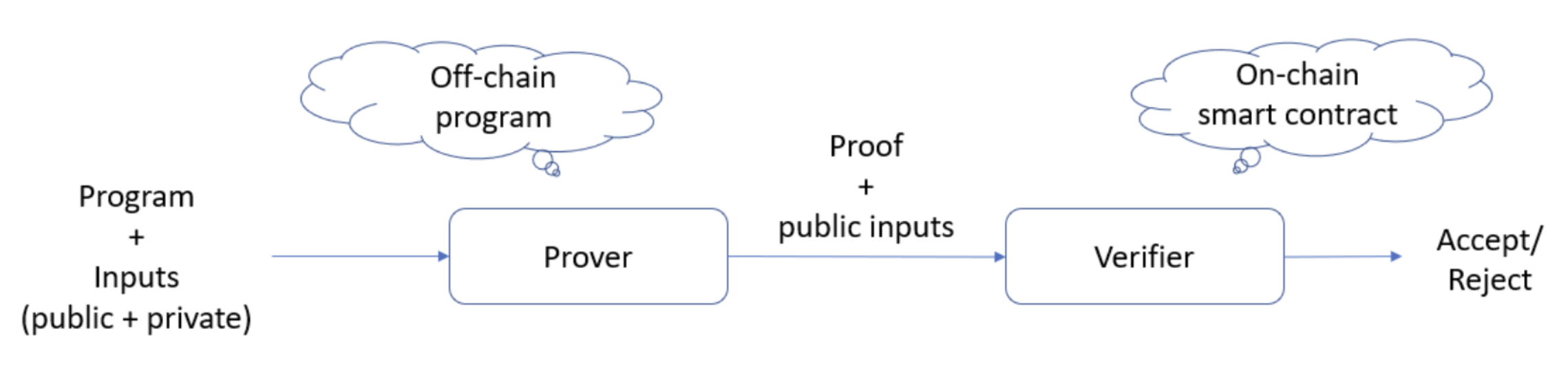
In the figure above, the program fed to prover can be anything, e.g., a voting system, a lottery game, Doom, whatever computing task you want to offload from L1 to L2.
Zero-knowledge Ethereum Virtual Machine (zkEVM)
Overview
zkEVM is an EVM that is verifiable. In short, the validity of any computation run on zkEVM can be verified through zero-knowledge proofs (or validity proofs). A fun fact about EVM is that it is quasi-Turing-complete (according to Ethereum Yellow Paper), which means EVM can perform pretty much any computation that respects the intrinsic bound set with gas. Hence, by making EVM verifiable, we have essentially made all computations on Ethereum's execution layer verifiable. This allows us to "outsource" most of the transaction processing job from Ethereum to L2 via ZK rollup.
Another way to think of zkEVM is as a special kind of ZK rollup (the program given to prover is EVM). From this viewpoint, we can divide zkEVM into two major parts:
- Logic Part:
- EVM program: EVM's logic expressed as ZK circuits
- Zero-knowledge Part:
- Prover: Off-chain program that generates proof given the EVM program and inputs
- Verifier: Smart contract that performs proof verification
- Data availability (DA).
- L2 Data availability ensures public verifiability, allowing anyone to verify transactions are executed correctly on L2.
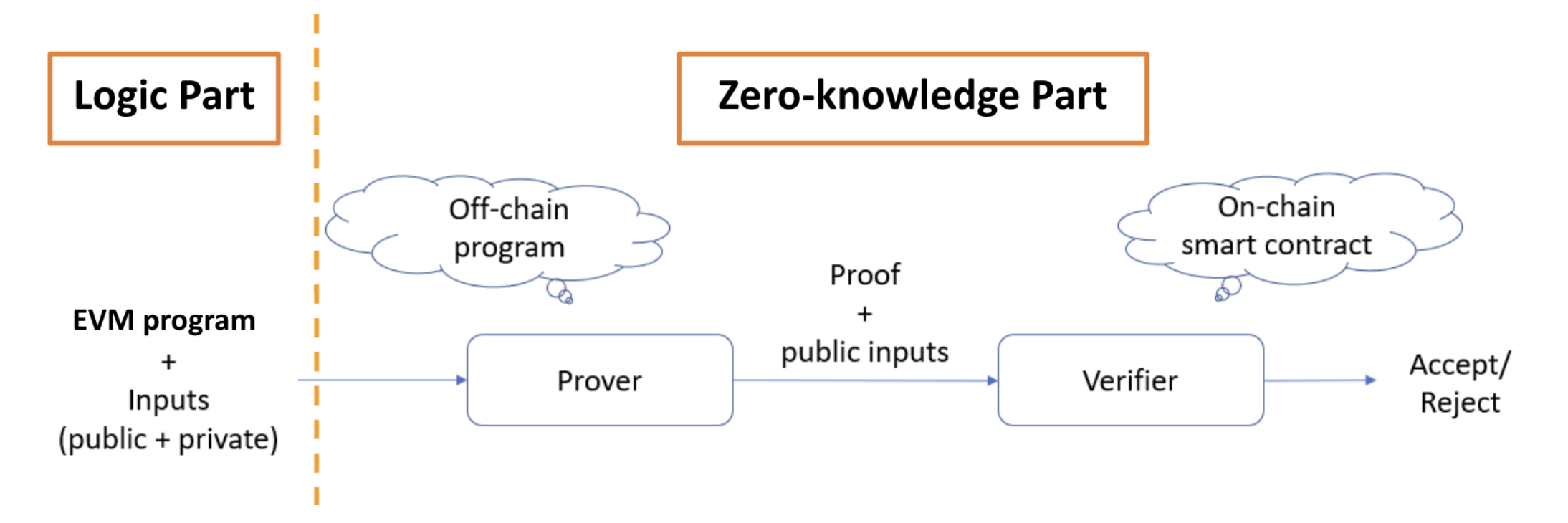
Simply put, the statement of zkEVM is something like: I have executed the EVM correctly with the given inputs. In reality, this statement must be formalized so that it can be "interpreted" by the zero-knowledge part of zkEVM (similar to how programmers must write code for computer to "understand" a task). We refer to said formal representation as ZK circuits.
The prover can only generate zero-knowledge proofs for statements of a certain format. In literature, this format is usually called circuits (or arithmetic circuits) due to its similarity to the regular electric circuits. To avoid confusion between these two types of circuits, we refer to the former one as ZK circuit. Depending on which proof system & implementation are used, the definition of ZK circuits may differ. A few examples are R1CS (used by snarkjs for PlonK, fflonk & Groth16), AIR (used by Winterfell for STARK), etc. Usually, programmers of ZK circuits express the logic in a higher-level language then compile it down to its circuit form. The process of converting a high-level program into ZK circuits is called arithmetization.
Beyond logic and zero-knowledge aspects, ensuring data availability is critical. This guarantees users can access their transaction data, safeguarding their assets even in scenarios involving malicious activities.
Another pivotal consideration is EVM compatibility. According to Vitalik Buterin, zkEVMs are categorized into four types based on their performance and compatibility with the EVM.
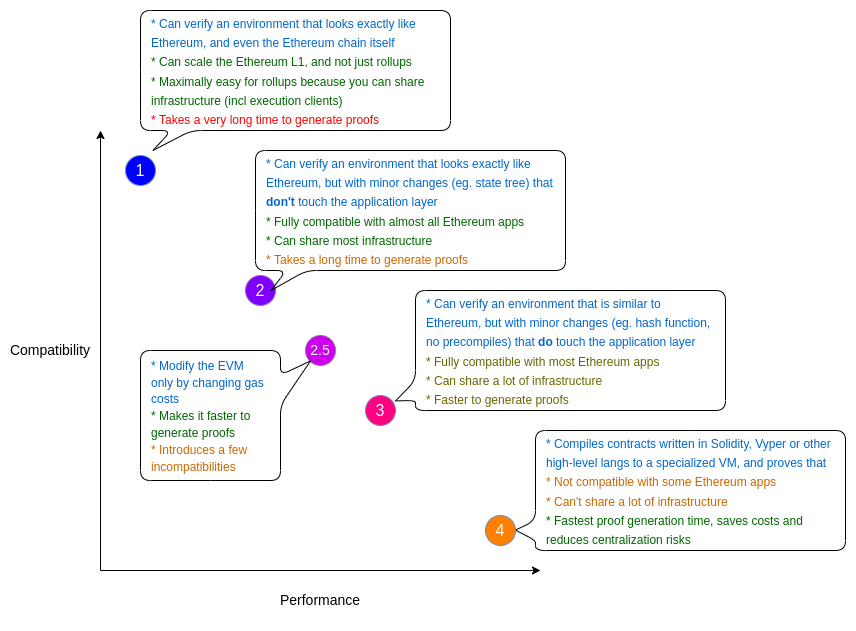
We are now examining two widely adopted and fully open-source zkEVMs: Polygon zkEVM and zkSync Era. We will begin by exploring the technical stack of each product, including their logical architecture, zero-knowledge components, and data availability (DA) solutions. Polygon zkEVM is primarily focused on optimizing fast proving times, aiming to expedite the verification process efficiently. In contrast, zkSync Era prioritizes data compression through its state diffs mechanism, which facilitates more economical on-chain settlement.
Furthermore, we will evaluate the EVM compatibility of both zkEVMs. Polygon zkEVM demonstrates high compatibility with EVM by directly interpreting EVM bytecode without the need for an intermediate representation. On the other hand, zkSync Era's instruction set differs significantly from EVM, preventing it from directly interpreting EVM bytecode like Polygon zkEVM.
This comparison highlights the distinct approaches and technical considerations of each zkEVM in the context of their architecture, zero-knowledge features, data availability solutions, and compatibility with Ethereum's EVM.
Polygon zkEVM
Polygon zkEVM is developed by Polygon Labs. Polygon Labs has open-sourced two implementations of their CPU prover (written in C++ and Javascript).
Logic Part: The logic part of Polygon zkEVM is divided into two parts: Polygon-VM and its ROM. Implementing logic part starts with a DSL called Polynomial Identity Language (PIL). This language is used to describe a uniprocessor VM. We refer to this machine as Polygon-VM. The firmware of Polygon-VM is written in a higher-level DSL called zero-knowledge Assembly (zkASM). The logic of EVM is contained within this firmware. Due to its immutability, the firmware is referred to as the read-only memory (ROM) of Polygon-VM.
Zero-knowledge Part: Polygon zkEVM generates proofs of CI through a pipeline. In this pipeline, eSTARK [8] is utilized to perform proof recursion, aggregation and composition while Groth16 [1] or fflonk [9] is employed for proof compression.
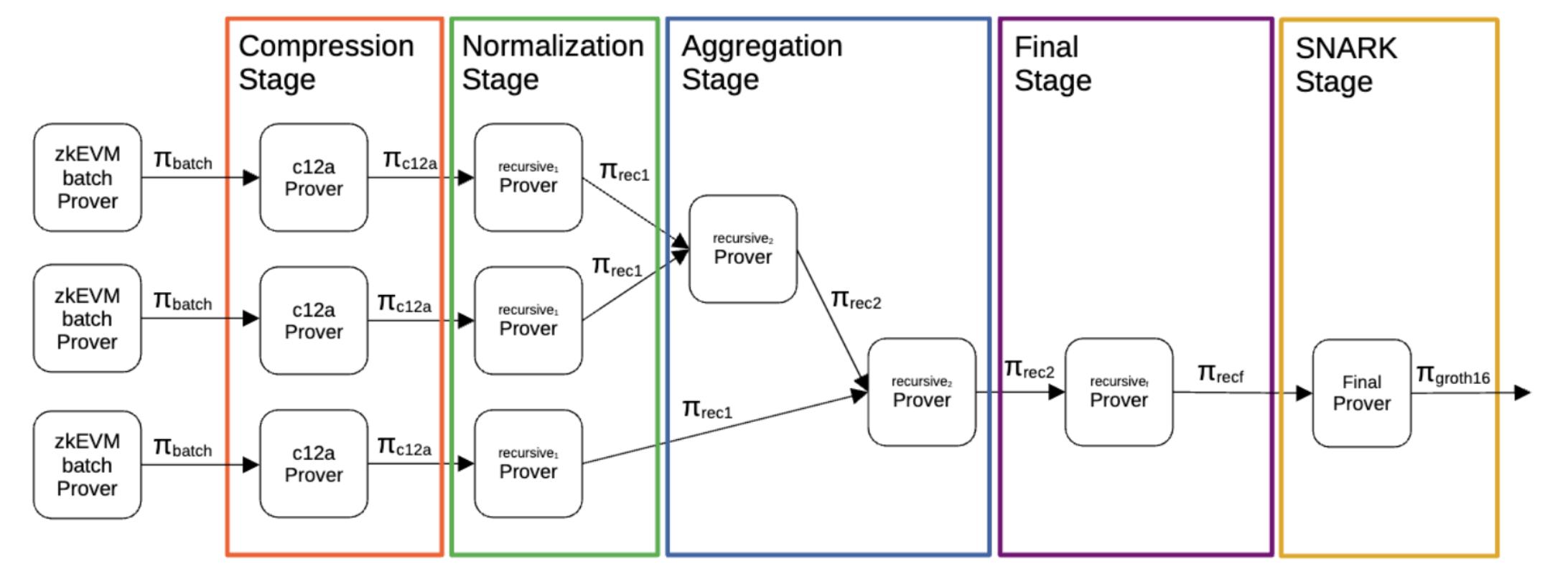
DA Solution: All transaction data of Polygon zkEVM is stored on Ethereum smart contracts. More specifically, RLP-encoded L2 transactions must be saved to rollup contract for them to be processed. This approach is simple to implement, and gives maximum transparency.
EVM Compatibility: Polygon zkEVM is nearly a full type-2 zkEVM, thanks to the Etrog update in early 2024. After Etrog update, dApps developers can redeploy their smart contracts exactly as they are on Ethereum without the need for additional auditing or modifications. As pointed out in Vitalik Buterin's blog, type-2 zkEVMs appear to be EVM-equivalent but they are, in fact, slightly different regarding some parts like block structure and state tree.
- Block structure: In Polygon zkEVM, multiple blocks (a.k.a. L2 blocks) are bundled into a batch. Unlike Ethereum blocks, Polygon zkEVM's L2 blocks do not contain any other data besides from the RLP-encoded transactions. A block consists of:
- Change-L2-block transactions: the deliminators for different blocks within the same batch
- Regular Ethereum transactions: at the time of writing, only legacy transactions are supported

- State tree: While the original EVM stores Ethereum's state in a Merkle-Patricia Trie constructed with Keccak256, Polygon zkEVM utilizes a Trie Binary Sparse Merkle Tree built with Poseidon-Goldilocks.
Polygon zkEVM's high compatibility with EVM is demonstrated by its ability to interpret EVM bytecode; no intermediate representation is required.
zkSync Era
zkSync Era is developed by Matter Labs. Matter Labs has open-sourced their CPU and GPU provers, namely era-boojum and era-shivini (both written in Rust).
Logic Part: Two main components of zkSync Era's logic part are Era virtual machine (EraVM) and system contracts. EraVM is a register-based VM written in Rust (based on the era-boojum library). Similar to modern operating systems, EraVM has a special feature called kernel mode in which privileged operations like calling system contracts are allowed. System contracts are smart contracts written in Solidity or Yul which can only be accessed by EraVM in kernel mode. Some logics of EVM are migrated to system contracts since it makes implementing native Account Abstraction (AA) easier. Moreover, writing smart contracts is much less of a hassle than building Rust ZK circuits.
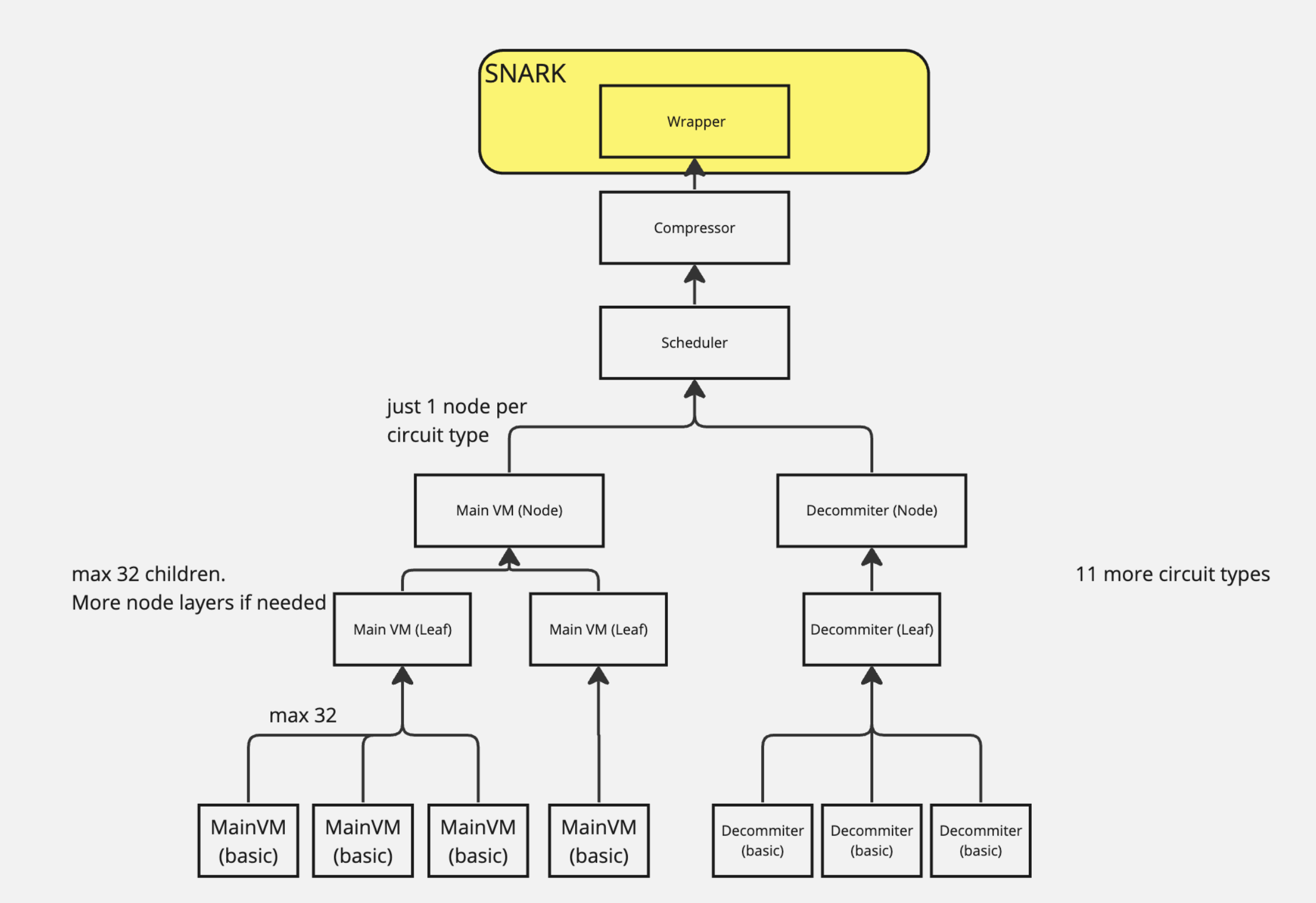
Zero-knowledge Part: zkSync Era uses a proof system called Boojum - an instantiation of RedShift [10]. A major source of inspiration for Boojum's design is Plonky2 - a transparent zk-SNARK tailored to fast recursive composition. In total, zkSync Era utilizes three types of ZK circuits: base-layer circuits, recursive-layer circuits and "AUX" circuits (see this document for more details). Overall, the proving architecture resembles a tree in which each node is a proof and every parent node is the aggregated proof of its children. zkSync Era's prover is able to scale horizontally as proof generation on base and recursive layers can be parallelized across a large cluster of CPUs or GPUs.
DA Solution: Instead of submitting detailed transaction data, zkSync focuses on posting state differentials ("state diffs") to L1. These diffs represent changes in the blockchain's state (account balance changes, storage updates, etc.), enabling zkSync to efficiently manage how data is stored and referenced:
- Instead of submitting detailed transaction data, zkSync focuses on posting state differentials (state diffs for short) to L1. These diffs represent changes in the blockchain's state (account balance changes, storage updates, etc.), enabling zkSync to efficiently manage how data is stored and referenced:
- Compression techniques: All data sent to L1, including state diffs, is compressed to further reduce costs.
EVM Compatibility: zkSync Era is classified as a type-4 zkEVM, which means compatibility is actively traded for faster development. To make comparison easier, we will examine the same aspects as we did for Polygon zkEVM.
- Block structure: In zkSync Era, there are two notions of blocks: L2 blocks and L1 batches.
- L2 blocks: blocks created on L2 (on the zkSync Era network). They are produced every few seconds, and not included on the Ethereum blockchain. An L2 block can contain a variety of transactions (legacy, EIP-2930, EIP-1559, EIP-712).
- L1 batches: batches of consecutive L2 blocks that contain all the transactions in the same order, from the first block to the last block in batch. As the name suggests, L1 batches are submitted to Ethereum.
- State tree: The state tree of zkSync Era is a single-level, full binary tree with 256-bit keys. Only changes of smart contract storage slots are written directly to state tree. The rest of Ethereum's state (account nonce, balance, code, etc) is managed by system contracts.
Since EraVM's instruction set is mostly different from that of EVM, it cannot interpret EVM bytecode directly like Polygon zkEVM. According to specification, EraVM only supports one native language called EraVM bytecode (a.k.a. zkEVM bytecode). In order to make this VM usable, the team at Matter Labs had to build a new toolkit for developers (zksolc/zkvyper for compilation, hardhat-zksync/foundry-zksync for debugging and testing). Compared to Polygon zkEVM, the compiler toolchain of zkSync Era is quite complicated.
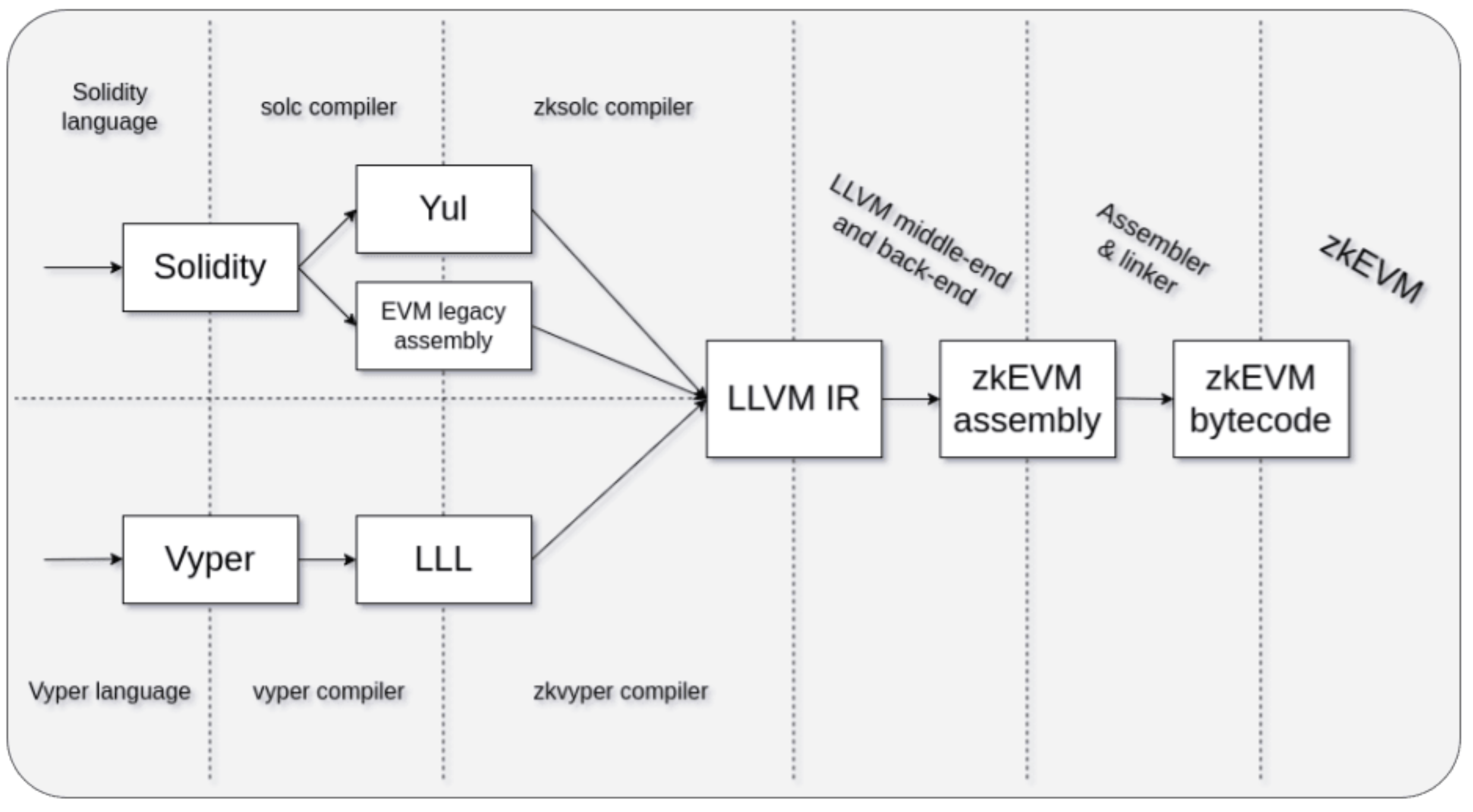
Besides incompatibility at bytecode level, zkSync Era also deviates from EVM in many aspects such as fee model, computer architecture, built-in Account Abstraction, etc. Notably, some of these changes actually alter the behavior of execution layer.
Performance benchmark
We present a benchmark comparison between Polygon zkEVM and zkSync Era based on data from [11].
Prover time. Polygon zkEVM maintains a proving time of either 190 or 200 seconds for each batch regardless of input size. In exchange for its outstandingly fast proof generation, Polygon zKEVM requires much more expensive hardware. On the other hand, the time spent on proof generation of zkSync Era extends with larger batch sizes. The proving time of zkSync Era increased from 400 to 1200 seconds when the batch size increased from 10 transactions to 200 transactions.
Settlement costs. This involves (a) calling the L1 contract to commit to a specific batch, and (b) submitting proofs and executing the verifier logic (e.g., SNARK verifier) for the committed batches.
| Metrics | Polygon zkEVM | zkSync Era |
|---|---|---|
| Median Gas per Batch | 59,434 gas | 816,275 gas |
| Median Batch Size | 27 | 3,895 |
| Median Batch Size | 2,201 gas | 209 gas |
Proof Compression. Some constructions involve compressing (or converting) the block’s proof from one proof system to another. This typically involves proving the verification of the aggregated proof in a cheaper (with regards to the verification cost) proof system (e.g., Groth16) so that the cost of settlement is lower. For Polygon zkEVM, the median time of proof compression is 311 seconds while the number for zkSync Era is 1,075 seconds.
DA costs One of the disadvantages of Polygon zkEVM is its high DA cost. The table below show the number of bytes used for DA
| Payload Type | Polygon zkEVM | zkSync Era |
|---|---|---|
| ERC-20 Transfers | 70,357 | 10,999 |
| Contract Deployment | 84,369 | 17,087 |
| ETH Transfer | 283,905 | 88,693 |
References
[1] Groth, Jens. "On the size of pairing-based non-interactive arguments." Advances in Cryptology–EUROCRYPT 2016: 35th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Vienna, Austria, May 8-12, 2016, Proceedings, Part II 35. Springer Berlin Heidelberg, 2016.
[2] Gabizon, Ariel, Zachary J. Williamson, and Oana Ciobotaru. "Plonk: Permutations over lagrange-bases for oecumenical noninteractive arguments of knowledge." Cryptology ePrint Archive (2019).
[3] Bowe, Sean, Jack Grigg, and Daira Hopwood. "Recursive proof composition without a trusted setup." Cryptology ePrint Archive (2019).
[4] Chiesa, Alessandro, Dev Ojha, and Nicholas Spooner. "Fractal: Post-quantum and transparent recursive proofs from holography." Advances in Cryptology–EUROCRYPT 2020: 39th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Zagreb, Croatia, May 10–14, 2020, Proceedings, Part I 39. Springer International Publishing, 2020.
[5] Ben-Sasson, Eli, et al. "Aurora: Transparent succinct arguments for R1CS." Advances in Cryptology–EUROCRYPT 2019: 38th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Darmstadt, Germany, May 19–23, 2019, Proceedings, Part I 38. Springer International Publishing, 2019.
[6] Ben-Sasson, Eli, et al. "Scalable, transparent, and post-quantum secure computational integrity." Cryptology ePrint Archive (2018).
[7] Polygon Zero Team et al. "Plonky2: Fast Recursive Arguments with PLONK and FRI"
[8] Masip-Ardevol, Héctor, et al. "eSTARK: Extending STARKs with Arguments." Cryptology ePrint Archive (2023).
[9] Gabizon, Ariel, and Zachary J. Williamson. "fflonK: a Fast-Fourier inspired verifier efficient version of PlonK." Cryptology ePrint Archive (2021).
[10] Kattis, Assimakis A., Konstantin Panarin, and Alexander Vlasov. "RedShift: transparent SNARKs from list polynomial commitments." Proceedings of the 2022 ACM SIGSAC Conference on Computer and Communications Security. 2022.
[11] Chaliasos, Stefanos, et al. "Analyzing and Benchmarking ZK-Rollups." Cryptology ePrint Archive (2024).
Disclaimer
Please note that this content is presented or otherwise made available to you on an “as is” basis for general informational and educational purposes only, without representation or warranty of any kind. This content should not be construed or used as financial, legal, or other professional advice, nor is it intended to recommend the purchase or use of any specific product or service. You must seek your independent advice from appropriate professional advisors. Where this article is contributed by a third party, please note that those views expressed belong to the third party and do not necessarily reflect those of Sky Mavis. Please refer to our Terms of Service for more information.

